
This in turn is equivalent to the proposition that. Theorem 8.1: If AC intersects BD at O (as in Figure 8.1), then AOB = DOC. AC with equality if and only if A, B, and C are collinear (on the same line). Let's prove a theorem using this two-column approach. As for definitions, it's enough just to give the term whose definition you are using. If your theorem or postulate wasn't special enough to warrant a name, you can either write down its number (they will all have numbers), or you can summarize the theorem. If your postulate or theorem was given a name (like the Angle Addition Postulate), all you have to write down is the name. In that case, all you need to include in your justification is “given.” In other cases, your justification will be a definition, a postulate, or a theorem. Sometimes the justification for your claim is that you were given the information. In the second column you write why you can make that claim. In the first column you write what you are claiming, step-by-step. It will help you organize your proofs and make them easy to read and understand. This technique has been used for centuries (or at least since I first learned geometry).
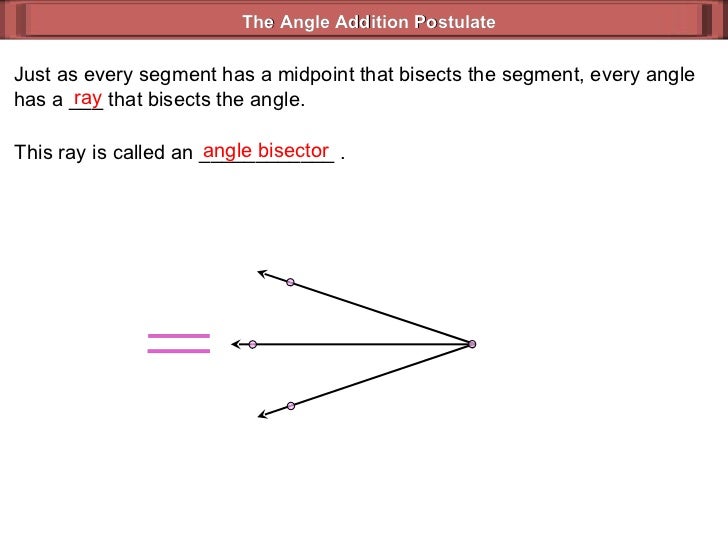
Write your proofs using the two-column technique. It will be obvious if substandard parts are used, and any shoddy workmanship will be apparent immediately. As long as you start with a firm foundation of definitions and postulates, your structure will weather any storm. You will build on what you've already established, and your house of cards will begin to stretch to the sky. The more theorems you have proven, the more sophisticated (and shorter) your proofs will become. When you construct a proof, go step-by-step from your given information to (hopefully) your conclusion, or what you want to prove, using only your definitions, postulates, and theorems. What Should You Bring to a Formal Proof?.A Solid Foundation: Definitions, Postulates, and Theorems.The Given Information: Use It or Lose It!.Proof by Contradiction: The Advantage of Being Indirect.The Segment Addition Postulate is similar to the angle addition postulate, but you are working with line segments instead of adjacent angles. These cables placed at specific angles support the bridge’s structure by sharing the weight of the bridge evenly across its supports. Some bridges have cables connected to bridges at angles from the bridge floor to towers. The Howe truss is made up of two 60° triangles and the Fink truss is made with three 40° triangles. It is important the angles in each triangle are measured correctly, as roof trusses provide support for a roof.
Roof trusses are beams of timber organized in triangles in the roofs of buildings. There are many applications of the postulate, especially in architecture and engineering. Now you know how the postulate works, you must know how it can be used in real life. Real-Life Application: Angle Addition Postulate

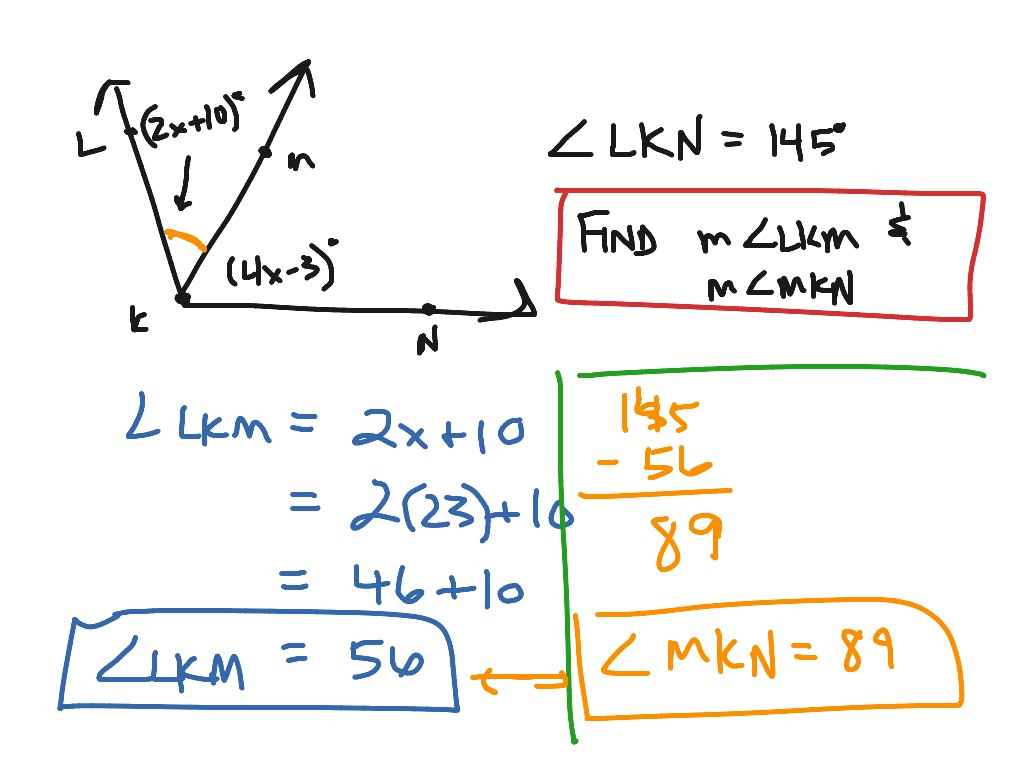
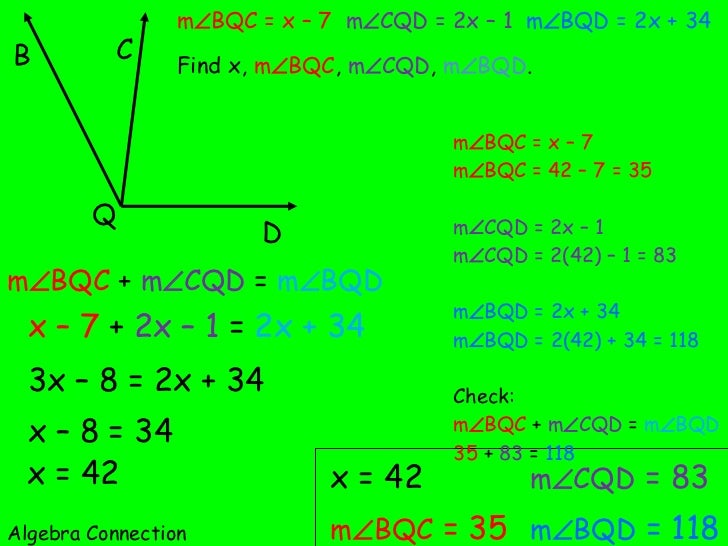
You can find their resulting angle as the sum of 90° and 30° so ∠JKM is 120°. The angle ∠JKL is a right angle so it is 90°, and from the diagram, you will see LKM is 30°. Now you know how the postulate works, let’s work through an example and calculate the resulting angle.Īs you can see these angles share the same side KL, so they are adjacent. However- notice how the resulting angle changes? This is because it is the sum of the two adjacent angles. You will find that changing points A, D, or C will affect the resulting angle it makes, without affecting the adjacent angle. Here’s a fun tool to play around with and explore how changing the size of two adjacent angles affects the size of their resulting angle.


 0 kommentar(er)
0 kommentar(er)
